Hallo Forenfreunde,

gestern bin ich im web auf ein zwar schon etwas älteres Video einer Experimentalphysik-Vorlesung von Prof. Walter Levin (MIT, Boston) gestossen, die mich zum Staunen gebracht hat. Der behandelte Stoff ist eigentlich physikalisches und elektrotechnisches Grundwissen, 1. Semester. Bessser gesagt, er sollte es sein. Das Thema ist Induktion und Messung induzierter Ströme und Spannungen - ganz elementar also. So eine Vorlesung habe ich auch mal besucht (lang ist es her...). Aber das, was hier zum Schluß ganz einfach abgeleitet und anschliessend vor den Hörern experimentell eindrucksvoll demonstriert wird, war mir neu. Das wurde mir seinerzeit jedenfalls so nie vor Augen geführt und auch in Lehrbüchern nicht in dieser Konsequenz.

Zwar heisst es korrekt in Wikipedia (de.wikipedia.org/wiki/Kirchhoffsche_Regeln) zu den Kirchhoffschen Regeln:
"Die Maschenregel ist formal eine Schlussfolgerung aus dem Induktionsgesetz. Sie gilt nur für den Fall, dass innerhalb der Masche keine Änderung des magnetischen Flusses erfolgt ... und somit auch auf magnetischem Weg keine Energie in das Netzwerk eingespeist oder von dort entnommen wird."

Die praktische Auswirkung daraus wird aber erst durch die augenöffnende Demonstration im Video im letzten Teil deutlich (ab 35:15 Min bis Ende):








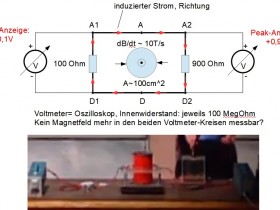
Ich war sozusagen "platt" zu sehen, dass die Potentialdifferenz zwischen zwei Punkten in einem elektrischen Kreis bei sich veränderndem Magnetfeld nicht eindeutig ist. Zwei Voltmeter gleichen Typs, beide an dieselben beiden Punkte A und D angeschlossen, können drastisch verschiedene Spannung anzeigen, ja sogar mit entgegengesetzter Polarität. Phänomenologisch ist das schwer begreiflich, dass die gemessene Spannung (Potentialdifferenz) zwischen zwei Punkten in einem Stromkreis davon abhängen soll, wie das Voltmeter (bzw. Oszilloskop) an eben diese Punkte angeschlossen ist. Physikalische Herleitung und praktische Demonstration im Video lassen offensichtlich keinen Zweifel zu.

Prof. Levin hat jedenfalls offensichtlich aus dem akademischen Umfeld Jahrzehnte lang Kopfschütteln und Unverständnis erfahren (mit nicht-wahrhaben- wollen der experimentellen Demonstration und physikalischen Begründung- Dogma über Wissenschaft). Den Äusserungen ist das anzumerken. Ich glaube, eines seiner letzen erklärenden Videos im Kampf gegen diese Ignoranz ist das hier, in dem er auf die vorgebrachten Einwände eingeht:



Aber dennoch....trotz der Logik...ganz verstanden habe ich es auch danach immer noch nicht, warum, ein Voltmeter bei unveränderter Schaltung und Abgriff an denselben Punkten A und D (bzw. A1 und A2 bzw. D1 und D2, die jeweils durch eine hinreichend induktionsarme und niederohmige Cu-Leitung verbunden sind, verschiedene Werte zeigen kann. Das Spannungsmessgerät "weiss ja nicht", ob es selektiv die Potentialdifferenz für die Stromrichtung A-->A2-->D2-->D oder für die Stromrichtung (path) D-->D1-->A1-->A anzeigen soll, selbst wenn diese beiden unterschiedlichen (Strom-) Richtungen die beiden unterschiedliche Potentialdifferenzen zwischen D und A bewirken.

Wie ist es einleuchtender zu erklären, dass es besser verständlich wird?
Oder wo ist der Fehler oder Trick im experimentellen Demo und Levin sitzt einer üblen Täuschung auf? Das klingt mir eigentlich nicht danach.

Was mir allerdings an dem Versuchsaufbau im ersten Video nicht gefällt:
1. Die Messleitungen zu den beiden Voltmetern / Oszilloskopen sind auf dem Tisch liegend flach aufgerollt (Induktivität!). In diesen so hergestellten Messleitungs-Spulen könnte vom äusseren Magnetfeld der Induktionsspule beim Einschalten der Induktionsspule ein Strom induziert werden, der die Anzeige des Messgeräts verfälscht.
2. Die Messleitung zum linken Oszilloskop ist weiter von der Induktionsspule entfernt aufgerollt als die rechte Messleitung.
3. Das linke Oszilloskop ist von der Induktionsspule auch weiter entfernt als das rechte. Das lässt vermuten, dass die Windungszahl der aufgerollten rechten Messleitung grösser ist als der rechten.
4. Wenn die Feldlinien der sehr kräftigen Spule ausreichend weit herausreichen und die aufgewickelten Messleitungen erreichen, wird in der näheren rechten Messleitung ggf. eine grössere Spannung induziert als in der linken.
5. Hängt die Polarität der vom Oszilloskop angezeigten Spannung auch von der Wickelrichtung der zur Spule gewickelten Messleitung ab?



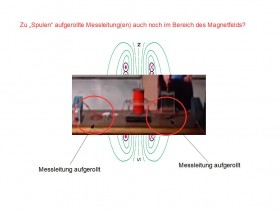
Im zweiten Video zur Entkräftung von Gegenargumenten erklärt Levin, dass die Leitungen vernachlässigbare Induktivität hätten. Seine Erklärung berücksichtigt aber nicht die erkennbare Wicklung zu je einer flachen Spule auf dem Experimentiertisch. Das macht mich etwas stutzig. Stimmt es wirklich, dass das Magnetfeld der induzierenden Spule nicht bis zu den Wicklungen der Messleitung reichen kann?

Auch:
Kennt Ihr praktische Konsequenzen/Beobachtungen bei Messungen in der Radiotechnik, die das experimentelle Resultat in den Videos bestätigt oder widerlegt?

Ich weiss nicht, ob ich hier einen "alten Hut" aufmache. Ich hoffe, nicht.
Einfach kann man das vorgeführte Experiment zu Hausevermutlich nicht nachstellen. Man müsste ja im Kreis mit den beiden Widerständen einen Strom von 1 mA induzieren, um am 900 Ohm Widerstand einen Spannungsabfall von 0,9V zu bekommen.

Wie seht Ihr das?


Gruß
Reinhard

Ich bin ja mit meinem Verständnisproblem nicht allein.
Im web wird das ebenfalls diskutiert - mit mehr oder weniger tauglichen Argumenten und Annahmen:

physics.stackexchange.com/ques…te-breakdown-of-intuition

Die Frage ist aber auch dort nicht übereinstimmend beantwortet.

Frage des Themenerstellers (Zitat):
"In Lewin's final diagram there are two voltmeters which, apart from a section of wire, attach in the same place. What happens as you bring the two attachment points together to meet? I can't see, in a physical on-the-table experiment, how one voltmeter is "measuring in the other direction"...."So, if I pick up either voltmeter and swing it over to the other side, without moving the attachment points, the value will change?"

In Deutsch (sinngemäß):
"In Lewins Schaltungsskizze sind zwei Voltmeter an die gleichen Stellen angeschlossen - abgesehen von einem Drahtstück dazwischen. Was würde passieren wenn man die beiden Anschlusspunkte aufeinander bringt? ich kann mir nicht vorstellen, daß in einem Vorführexperiment eines der Voltmeter eine umgekehrte Polarität anzeigen kann."..."Wenn ich ein (dort) angeschlossenes Voltmeter nehme und es einfach auf die andere Seite schwenke ohne die Anschlusspunkte zu verändern, verändert sich dann die Anzeige?"

Eine Antwort dort ist:
So ist es. Wenn das Voltmeter von einer Seite auf die andere geschwenkt wird, liegt dazwischen ein Punkt, an dem die von den Voltmeter-Messleitungen umfasste offene Fläche parallel zu den magnetischen Feldlinien steht. D.h. dann gibt es keinen magnetische Fluss durch die Fläche und die induzierte Spannung muss Null sein. Wenn also die Fläche, die von dem Voltmeter-Kreis aufgespannt wird, (um 180°) gedreht wird, fällt die induzierte Spannung vom positiven Wert auf Null (90°) und dann weiter auf einen negativen Wert (180°).

Das ist m.E. eine einleuchtende Begründung. Sie wird nur leider von Prof. Lewin selbst in seinem Video, in dem er auf Argumente seiner Kritiker eingeht, dadurch negiert, indem er sagt "der Voltmeter-Kreis umschliesse das
sich ändernde Feld NICHT und deshalb reiche es aus, nur den Kreis mit den beiden Widerständen zu betrachten, das die Spule umgibt. Eine vollständige Behandlung, in der die beiden Voltmeter-Teil-Kreise zusätzlich berücksichtigt werden, führten zum gleichen Ergebnis."

Und genau dort liegt ein Mangel in der Art der Erläuterung von Lewin, da sie zu einem Missverständnis einlädt. Denn da die Anzeige von der Position des Voltmeters relativ zur Spulenseite (besser: von der Lage der von den Leitern im Voltmeterkreis umschlossenen Fläche relativ zum sich ändernden Magnetfeld) abhängt, muss diese Fläche ein sich änderndes Magnetfeld umschliessen (Faraday). Umfasst sie nämlich kein Magnetfeld gilt Kirchhoffs Regel und dann kann die Anzeige nicht von der Lage des Voltmeters oder der Führung der Messleitung (path) abhängen. D.h. dann müsste man das Voltmeter von rechts nach links schwenken können, ohne dass sich die Anzeige ändert. Man hätte dann aber mit dem Problem zu kämpfen, welche Spannungsanzeige das Voltmeter dann anzeigen sollte....IR2, 0V oder -IR1?

Für rechnerische Zwecke ist die Aufteilung in zwei Voltmeterkreise (Loop 1 und Loop 3), die isoliert gesehen der Kirchhoffschen Regel folgen und dem zentralen Induktionskreis (Loop 2), der dem Faraday-Gesetz folgt, nützlich und liefert das richtige Ergebnis. Für das konzeptuelle Verständnis ist diese Aufteilung aber eher hinderlich. Man darf ja nicht ausser acht lassen, dass ohne die Induktion das Voltmeter nichts anzeigen würde, das Magnetfeld auch vom Voltmeterkreis umschlossen wird, sonst kann man schwer verstehen, warum das "Herüberheben" des Voltmeters auf die andere Seite die Anzeige ändert. Das kommt einem ja sowieso fast wie Zauberei vor.

Besser für das Verständnis ist, denke ich, diese Analyse und sie liefert das gleiche Endergebnis:

Der Innenwiderstand Ri des Voltmeters wird als Parallelwiderstand zum zugehörigen Widerstand auf der jeweils gleichen Seite behandelt. Faktisch ist dies natürlich der Lewin-Analyse gleichwertig, da der Gesamtwiderstand R* aus den Parallelwiderständen R_i (Voltmeter-Innenwiderstand) und R2 (bzw. R_i und R1 auf der anderen Seite) damit nach Kirchhoff 1/R* = 1/[(1/R2)+(1/R_i)] ist. R2 ist in dieser Behandlung ein Shunt zum Voltmeter. Damit hängt man nicht an der Vorstellung, der Voltmeterkreis würde nicht das veränderliche Magnetfeld umschliessen und die Position des Voltmeters, bzw. seiner Messleitungen könnten das Anzeigeergebnis nicht beeinflussen. Denn solche Vorstellung lässt ja nicht verstehen, wieso ein "Flip-Over" des Voltmeters mit seinem Leitungskreis auf die "andere Seite" die angezeigte Spannung ändert. Hat man aber das Induktions-Magnetfeld umschlossen, kann man es schon verstehen.

Man kann nun die übrige Rechnung wie gewohnt nach Faraday aufmachen:



Da ja Ri 100 MegOhm ist, kann schliesslich 1/Ri gegenüber 1/R1 bzw, 1/R2 vernachlässigt werden und man kommt rechnerisch auf dasselbe Ergebnis wie Lewin, nämlich dass das rechte Instrument V2= EMF- R₁I = +0,9V anzeigen muss und das linke Instrument V1 = -(EMF-R₂I)= -0,1V, wenn R1= 100Ohm, R₂=900 Ohm und EMF = 1V ist. In der Abbildung gezeigt für das rechte Instrument. Für das linke Instrument geht das entsprechend und liefert V1 = -(EMF-R₂I).

Lewin hat es also nur etwas unglücklich erklärt. Nun kann ich es verdauen. Hat mir keine Ruhe gelassen!


Habt Ihr Kommentare / Ergänzungen?


Gruß
Reinhard

PS Nachtrag 06.092018
Meine hier gezeigte alternative "Rechnung" ist - wie auch die von Prof. Lewin in seiner Vorlesung gegebene - unvollständig und nicht hinreichend, da sie die im Kreis induzierte EMF nicht korrekt berücksichtigt. Die vollständige experimentelle Antwort wird von Cyriel Mabilde im weiter unten verlinkten Video gegeben und die physikalische Abhandlung dazu im letzen Link (physicsforums.com/insights/a-n…dr-walter-lewins-paradox/)

Dieses nicht-intuitive Experiment ist in fast gleicher Art bereits 1982 von Prof. Robert H. Romer, Physics Department, Amherst College, Amherst, Massachusetts, publiziert worden:

Robert H. Romer
American Journal of Physics 50 (12), Seiten 1089-1093, 1982

als pdf verfügbar:

http://www.phy.pmf.unizg.hr/~npoljak/files/clanci/guias.pdf










Die Änderung des induzierenden Magnetfelds der Luftspule wird hier durch Dreieckmodulation des Spulenstroms bewirkt und im Oszillogramm als obere Kurve durch den entsprechenden Spannungsabfall an einem Serienwiderstand in der Spulenstromversorgung wiedergegeben. Daraus resultieren Rechtecksignale des Spannungsabfalls der induzierten EMF über die beiden Widerstände R1 und R2. Auch hier sieht man die Vorzeichenumkehr und die betragsmässige unterschiedliche Anzeige der beiden Oszilloskope entsprechend des jeweiligen Spannungsabfalls über R1 und R2, obwohl beide Oszilloskope an genau denselben Punkten mit der Topologie wie in der obigen Abbildung angeschlossen sind.



Hier ist dann auch noch ein weiteres erhellendes Experiment vorgestellt:

Eine Messleitung des linken Oszilloskop wird anders verlegt, nämlich wie nachfolgend abgebildet. Die beiden Anschlusspunkte sind unverändert. Mit dieser geänderten Topologie der Verlegung des Anschlusses zeigen beide Instrumente gleich an:



Es kommt also - wie auch zu erwarten - sehr wohl darauf an, wie die Anschlussleitungen zum Voltmeter verlegt sind.

Auch die kritik an der in Lehrbüchern oft fehlerhaft dargestellte Anwendung von Kirchhoffs Regeln im Falle von Induktion und Selbstinduktion sind dort bereits enthalten. Prof. Lewin hat dies offensichtlich wieder aufgegriffen - oder unabhängig nochmals und zufällig in gleicher Weise thematisiert.


Reinhard

Forenfreunde,
...wenn Ihr das Interesse noch nicht verloren habt....

Die bisherigen Erklärungen sind immer noch nicht vollständig zufriedenstellend.
Soweit war es bis hier:

1) Die Voltmeter-Kreise umschliessen ebenfalls den magnetischen Fluss, wenn sie ausserhalb der Spule, so wie bei den gezeigten Experimenten positioniert sind. Anders ist die gefundene Abhängigkeit der angezeigten Spannung von der Topologie (Orientierung) der Messleitungen) des Voltmeters nicht möglich. Das ist von Lewin unbeachtet geblieben, mit der Begründung, daß ausserhalb der Spule praktisch kein magnetischer Fluss mehr messbar gewesen sei. Die Stichhaltigkeit seiner Behauptung ist zumindest fraglich, jedenfalls nicht von ihm demonstriert.
2) Der Einfluss des magnetischen Flusses auf den Voltmeterkreis ist nur dann vermeidbar, wenn der Voltmeter-Anschluss mit dem Messgerät keiner Änderung des magnetischen Flusses ausgesetzt ist, in ihnen selbst also keine EMF induziert wird. Dies bedingt mindestens die Orientierung der Messleitungen in der Weise, dass die magnetischen Feldlinien die vom Voltmeterkreis aufgespannten Fläche nicht durchdringen (also längs der Spulenachse, parallel zu den Feldlinien).


Folgende Fragen noch offen:

A) In einem Transformator kann ein relativ geringer Ohmscher Widerstand über die Wicklung vorliegen und dennoch an den offenen Enden eine hohe Spannung erzeugt werden.Ist die Annahme dann immer richtig, dass bei einem kleinen oder vernachlässigbaren Ohmschen Widerstand keine keine Potentialdifferenz ("Spannung") in dem Leiter im veränderlichen Magnetfeld sein könne?

a1) Sollte es dann nicht einen Unterschied machen, wenn die Messleitung zum Voltmeter an den Punkten A1, A oder A2 angeschlossen wird (dasselbe gilt für D1, D, D2)?
In den Darstellungen von Lewin und Romer wurde das verneint, da im Experiment nicht festgestellt wurde, dass der Anschluss der Messleitungen an die Punkte A1, A und A2 einen Unterschied macht.



a2) Wird mit dem Voltmeter wirklich zwischen A1 und A2 keine Spannung gemessen?
a3) Falls zusätzlich ein Widerstand in Serie liegt, sollte der Spannungsabfall über diesem Widerstand (=I.R) der magnetisch induzierten EMF in dem gewählten Segment entgegenwirken. Es sollte also der Nettoeffekt von beiden gemessen werden können?

B) Wenn im vorliegenden Fall (Lewin Experiment) mit R1=100 Ohm, R2=900 Ohm) die Voltmeter an die Punkte A und D (also "mittig") angeschlossen sind, und zwar in der Weise, dass die Messleitungen, die mit dem Voltmeter den Voltmeterkreis bilden, keiner Änderung des Magnetfelds ausgesetzt sind, also parallel zu den Magnetfeldlinien positiniert sind (von den Messleitungen aufgespannte Fläche ist längs der Spulenachse), welche Spannung wäre dann zwischen A und D zu messen?


Ich hatte diese Fragen nirgendwo beantwortet und experimentell überprüft gesehen und war schon in der Vorbereitung, das selbst nachzuprüfen, als ich heute ein wunderbares Video des Belgischen Elektrotechnikers/Ingenieurs Cyrie Mabilde gefunden habe, der genau diesen Fragen und noch mehr nachgegangen ist und in bemerkenswerter Weise untadelige experimentelle Aufbauten verwendet hat, die eine vollständige, wirklich umfassende Erklärung geben.

Die Quintessenz:
1. Kirchhoffs Regeln sind doch gültig, man muss sie nur vollständig und konsequent anwenden (McDonald, Lit. s. weiter unten).
2. Der experimentelle Aufbau in der Vorlesung von Lewin ist schlecht geignet, Klarheit in die Zusammenhänge zu bringen. Dies hat jetzt das hier unten verlinkte Video von Mabilde geleistet.
3. Die Messung der sog. "skalaren Potentialdifferenz", wie von Mabilde eindrucksvoll demonstriert, trägt wesentlich zum Gesamtverständnis bei. Es kann "von aussen (ausserhalb der Spule) nicht gemessen werden.

Seht Euch das Video an, wirklich sehenswert!




Eine Publikation zu diesem sog. "Lewin Paradox" ist daraufhin erst vor kurzem von Prof. Kirk McDonald von der Princeton University, New Jersey erschienen. Das Thema hat also hochrangige Experten bis jetzt bewegt. Auch er zitiert die Ergebnisse im Video von Cyrie Mabilde.

hep.princeton.edu/~mcdonald/examples/lewin.pdf

Damit ist das "Problem" wohl umfassend geklärt. Keine Fragen mehr offen!

Ist über dies traurig zu sehen, dass Prof. Lewin, ein ehemals in Wissenschaft und Lehre hoch respektierter Hochschullehrer am angesehenen Massachusetts Institute of Technology, mit vielen wissenschaftlichen Auszeichnungen, nicht in einen tieferen sachbezogenen wissenschaftlich-technischen Dialog in dieser Sache eintreten wollte, um Transparenz herzustellen und vermeintliche oder tatsächliche Widersprüche aufzuklären. Aber das ist ja wieder ein ganz anderes Thema.

Dazu eine neue physikalische Herleitung, die sowohl das Mabilde-Video als auch die McDonald Publikation berücksichtigt.
A New Interpretation of Dr. Walter Lewin’s Paradox, June 25, 2018/16; Comments/in Physics /by rude man
physicsforums.com/insights/a-n…dr-walter-lewins-paradox/


Was mich an diesem Thema bewegt hat:
Ist es nicht faszinierend, welche Wellen, Diskussionen und Dispute ein einfaches Induktionsexperiment mit einer Spule (primär) und einer sekundaren (1-loop) "Spule" und zwei Voltmetern noch bis in das jetzige Jahr (2018) schlagen kann? Immerhin 173 Jahre nach der Publikation von Kirchoffs Regeln und 145 Jahre nach Maxwells Publikationen zum Elektromagnetismus.


Reinhard

Obwohl der Disput ja bereits aufgelöst ist:
physicsforums.com/insights/a-n…dr-walter-lewins-paradox/
hep.princeton.edu/~mcdonald/examples/lewin.pdf


...geht jetzt die Fetzerei zwischen den Kritikern und Prof. Lewin weiter:

Electroboom: "Doch, Kirchhoff's Regel funktioniert!"


Und darauf die immer wiederholte, schmale Antwort von Prof. Lewin: "Kirchoffs Regel gilt nicht bei induzierter EMF. ...Im Falle eines elektromagnetisch induzierten Felds hängt die Potentialdifferenz vom Weg ab" (damit ist er immer auf der sicheren Seite, ohne konkret auf die Experimente und Interpretationen seiner Kritiker einzugehen).
Hier zitiert Prof. Lewin nun erstmals auch die frühere Publikation von Romer, 1982:




Man kann gespannt sein, ob es im weiteren Verlauf noch eine gemeinsame Basis geben wird, die ja, wie oben verlinkt, auf dem Tisch liegt. Der Zoff geht jedenfalls ungeachtet dessen erstmal weiter. Dabei ist es so einfach, wie ja McDonald bereits geschrieben hatte. Die Kirchhoffsche Regel wird gemäss einfach um die induzierte EMF erweitert. Kirchhoff konnte zu seiner Zeit elektromagnetisch induzierte EMF ja noch nicht in seine Regel einbeziehen, da sie erst seit Faraday bekannt ist. Warum wehrt sich Prof. Lewin so dagegen, das auch so zu sehen?

Reinhard

Ist das jetzt der Schluss? Oder kommt noch etwas von Prof. Lewin nach?
Zu seiner Sichtweise bekommt Electroboom Unterstützung und Bestätigung von Prof. J.W. Belcher (MIT, Boston, USA), Zitat unten.




Darin zitiert (zum öffnen der Links "Webseite verlassen" bestätigen, da die URL's ausserhalb youtube verweisen):

youtube.com/redirect?q=http%3A…description&v=Q9LuVBfwvzA

youtube.com/redirect?q=http%3A…description&v=Q9LuVBfwvzA

youtube.com/redirect?q=http%3A…description&v=Q9LuVBfwvzA


Reinhard

Das Thema beschäftigt weiterhin Elektrotechniker und Physiker, obwohl das Paradoxon ja schon aufgeklärt ist.

Prof. Lewin (ehem. Professor für Physik am ehrwürdigen Massachusetts Institute of Technology, MIT / Boston) wirft Fachkollegen der Physik und Elektrotechnik, die ihm widersprechen vor, sie würden ignorieren was sie sehen...sie sollten endlich akzeptieren, dass in einem sich verändernden magnetischen Feld Kirchhoffs Regel ungültig wär,alle Physik- und Elektrotechnik-Lehrbücher müssten deshalb umgeschrieben werden!

Die ihm widersprechende Fraktion wirft Prof. Lewin vor, er habe das Ohm'sche Gesetz nicht verstanden und würde es falsch anwenden! Es zeichnet sich ab, sie haben Recht. WOW, ein MIT-Physikprofessor, der das Ohm'sche Gesetz falsch anwendet.

Diese Geschichte wird wohl in die Physik / Elektrotechnik eingehen als das "Lewin Paradoxon"....oder so ähnlich!
Wie Ihr im ersten der drei unten angefügten Videos seht und hört, ist die "Lewin Clock" bereits nach ihm benannt - mit der das Phänomen elegant vorgeführt werden kann.


Immerhin, was man daraus mit nach Hause nehmen kann (und sich hinter die Ohren schreiben):

Zwei Voltmeter oder zwei Oszilloskope, die an denselben Messpunkten angeschlossen sind, können trotzdem völlig verschiedene Spannungen anzeigen, wenn ein magnetisches Wechselfeld in deren Zuleitungen (dem Stromkreis, in dem das Voltmeter oder Oszilloskop liegt) unterschiedliche Spannungen (Ströme) induziert, wenn die von den aufgepannten Zuleitungen (Leitern) aufgespannten Flächen z.B. in Lage (Winkel zum induzierenden Magnetfeld), Umfang, usw. verschieden sind.

Und selbst längs eines Leiters mit beliebig niedrigem Widerstand können jeweils zwischen zwei verschiedenen Punkten an diesem Leiter verschiedene Spannungen gemessen werden, je nachdem, wo sich die beiden Punkte befinden, wenn ein sich veränderndes magnetisches Feld in dem Leiter eine Spannung induziert.


Neue Videos dazu:








Reinhard