Hallo Reinhard, hallo Mitleser,
der Eingangswiderstand der ZF-Schaltung liegt, nicht wie bisher angenommen bei 4,7 kOhm, sondern bei etwa 500 Ohm. Das Praxisergebnis deckt sich bei mir auch mit der Simulation. Die blaue Kurve gehört zum in Reihe zur idealen Signalquelle geschalteten Widerstand von 500 Ohm. Dieser Wert ergibt hier 6 dB Pegelverlust, Anpassung. Bei 4,7k ist der Pegelverlust viel höher.
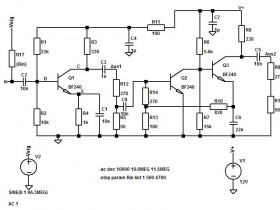
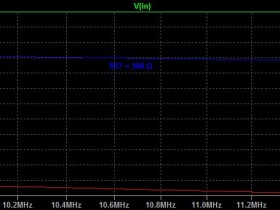
Was sich aber mit der bisherigen Simulation deckt, ist der notwendige Quellenwiderstand von 47 kOhm für die Primärseite des Filters. Ich habe mit einem 10 µH-Filter und 22pF einen Schwingkreis aufgebaut und über 47 kOhm angeregt. Unter diesen Bedingungen beträgt die -3db-Bandbreite ca. 300 kHz, wie gewünscht.
Ansonsten habe ich die letzten Stunden damit verbracht, eine ZF-Filterspule umzuwickeln, die Induktivitäten primär und sekundär zu messen, nochmals umzuwickeln, Koppelfaktor bestimmen...
Das Ergebnis sieht so aus:

Primärseitig sind es 30 Windungen, von oben bis kurz vor das untere Ende des Wicklungsraumes, um auf 10 µH zu kommen. Der Ferritkern reicht bis ca. zur Hälfte des Wicklungsraumes. Die unteren Windungen sind also noch frei.
Die Sekundärseite besteht aus 14 Windungen, ganz am unteren Ende des Wicklungsraumes gedrängt und etwas wild gewickelt. Sie ist damit relativ weit vom Ferrit weg, um eine geringe Kopplung zu erreichen.

Hier mit Ferritschirm und angeklemmten Kurzschlussleitungen für die Sekundärseite während der Bestimmung des Koppelfaktors.
Für die Messungen der Primärseite habe ich einen 22pF-Kondensator parallel angelötet, eine Seite mit 47 kOhm gespeist und die Frequenz des Meßgenerators auf Pegel-Maximum eingestellt. Nach der Thomson-Schwingkreisformel ergab sich eine Induktivität von 10,5 µH. Bei kurzgeschlossener Sekundärwindung lag der Wert ein wenig niedriger und ergab über die Formel
K= Wurzel (1- (L_kurzgeschlossen/L_offen)) einen Kopplungsfaktor von 0,20 - 0,25, je nach Kernstellung.
Die Sekundärspule weist mit ihren 14 Windungen eine Induktivität von 1,4 µH auf.
Das passt ganz gut, L1/L2 = (N1/N2)^2 umgestellt ergibt: N1 = N2 x Wurzel (L1/L2). Damit komme ich auf 11,2 Windungen. Es sind etwas mehr erforderlich, da der induktivitätserhöhend wirkende Kern in die Sekundärspule nicht eintaucht.
Die Simulation mit diesen Werten zeigt eine Bandbreite von ca. 400 kHz, da die Bedämpfung durch den Eingangswiderstand des ZF-Verstärkers rückwirkt. Man kann dem gegenwirken und auch noch etwas Pegel in der ersten Stufe herausholen, indem man den Emitterkondensator kleiner wählt. Sein Blindwiderstand, vergrößert durch die wirksame Stromverstärkung des Transistors, bestimmt wesentlich den Eingangswiderstand. Kleinere C-Werte vergrößern diesen und sorgen so für einen höheren Eingangspegel und geringere Rückwirkung und damit auch eine geringere Bandbreite. Sie verringern aber auch die Verstärkung der Stufe. Die Simulation gibt als Optimum 2,2 nF aus.
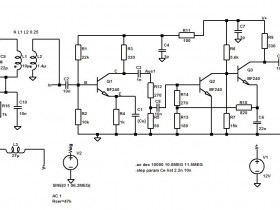
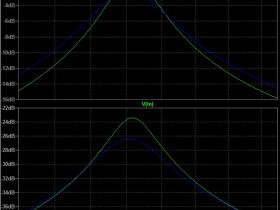
Die blauen Kurven gehören zu 10 nF für C1, der grüne Verlauf zu 2,2 nF.
Die Praxisprüfung muss das natürlich erhärten.
Viele Grüße,
Christian
der Eingangswiderstand der ZF-Schaltung liegt, nicht wie bisher angenommen bei 4,7 kOhm, sondern bei etwa 500 Ohm. Das Praxisergebnis deckt sich bei mir auch mit der Simulation. Die blaue Kurve gehört zum in Reihe zur idealen Signalquelle geschalteten Widerstand von 500 Ohm. Dieser Wert ergibt hier 6 dB Pegelverlust, Anpassung. Bei 4,7k ist der Pegelverlust viel höher.
Was sich aber mit der bisherigen Simulation deckt, ist der notwendige Quellenwiderstand von 47 kOhm für die Primärseite des Filters. Ich habe mit einem 10 µH-Filter und 22pF einen Schwingkreis aufgebaut und über 47 kOhm angeregt. Unter diesen Bedingungen beträgt die -3db-Bandbreite ca. 300 kHz, wie gewünscht.
Ansonsten habe ich die letzten Stunden damit verbracht, eine ZF-Filterspule umzuwickeln, die Induktivitäten primär und sekundär zu messen, nochmals umzuwickeln, Koppelfaktor bestimmen...
Das Ergebnis sieht so aus:
Primärseitig sind es 30 Windungen, von oben bis kurz vor das untere Ende des Wicklungsraumes, um auf 10 µH zu kommen. Der Ferritkern reicht bis ca. zur Hälfte des Wicklungsraumes. Die unteren Windungen sind also noch frei.
Die Sekundärseite besteht aus 14 Windungen, ganz am unteren Ende des Wicklungsraumes gedrängt und etwas wild gewickelt. Sie ist damit relativ weit vom Ferrit weg, um eine geringe Kopplung zu erreichen.
Hier mit Ferritschirm und angeklemmten Kurzschlussleitungen für die Sekundärseite während der Bestimmung des Koppelfaktors.
Für die Messungen der Primärseite habe ich einen 22pF-Kondensator parallel angelötet, eine Seite mit 47 kOhm gespeist und die Frequenz des Meßgenerators auf Pegel-Maximum eingestellt. Nach der Thomson-Schwingkreisformel ergab sich eine Induktivität von 10,5 µH. Bei kurzgeschlossener Sekundärwindung lag der Wert ein wenig niedriger und ergab über die Formel
K= Wurzel (1- (L_kurzgeschlossen/L_offen)) einen Kopplungsfaktor von 0,20 - 0,25, je nach Kernstellung.
Die Sekundärspule weist mit ihren 14 Windungen eine Induktivität von 1,4 µH auf.
Das passt ganz gut, L1/L2 = (N1/N2)^2 umgestellt ergibt: N1 = N2 x Wurzel (L1/L2). Damit komme ich auf 11,2 Windungen. Es sind etwas mehr erforderlich, da der induktivitätserhöhend wirkende Kern in die Sekundärspule nicht eintaucht.
Die Simulation mit diesen Werten zeigt eine Bandbreite von ca. 400 kHz, da die Bedämpfung durch den Eingangswiderstand des ZF-Verstärkers rückwirkt. Man kann dem gegenwirken und auch noch etwas Pegel in der ersten Stufe herausholen, indem man den Emitterkondensator kleiner wählt. Sein Blindwiderstand, vergrößert durch die wirksame Stromverstärkung des Transistors, bestimmt wesentlich den Eingangswiderstand. Kleinere C-Werte vergrößern diesen und sorgen so für einen höheren Eingangspegel und geringere Rückwirkung und damit auch eine geringere Bandbreite. Sie verringern aber auch die Verstärkung der Stufe. Die Simulation gibt als Optimum 2,2 nF aus.
Die blauen Kurven gehören zu 10 nF für C1, der grüne Verlauf zu 2,2 nF.
Die Praxisprüfung muss das natürlich erhärten.
Viele Grüße,
Christian
**************************************************
2 + 2 = 5 (für extrem große Werte von 2)
2 + 2 = 5 (für extrem große Werte von 2)

 Ich habe es jetzt mit meiner Methode nachgerechnet und komme nun auch auf 500 Ohm, wie Du. Ich habe keinen Schimmer, wo ich vorher den Fehler bei der Berechnung der Eingangsimpedanz gemacht hatte.
Ich habe es jetzt mit meiner Methode nachgerechnet und komme nun auch auf 500 Ohm, wie Du. Ich habe keinen Schimmer, wo ich vorher den Fehler bei der Berechnung der Eingangsimpedanz gemacht hatte.  Und da es hier um alte Radios geht, hat eine sachliche Fehleinschätzung nie wirklich tragische Konsequenzen.
Und da es hier um alte Radios geht, hat eine sachliche Fehleinschätzung nie wirklich tragische Konsequenzen.