Forenfreunde,

die im Titel gestellte Frage liest sich zunächst trivial.

Neben sog. harmonischen Verzerrungen, die als Klirrfaktor oder THD (total harmonic distortion) gemessen werden, treten beim Vorhandensein von mehr als einer Ton-Frequenz an gekrümmten Kennlinien von Bauteilen in Schaltungen (wie. z.B. bei einer Diode) auch sog. Intermodulationsverzerrungen auf. Das sind Mischprodukte, neue Signale, die bei Summen-und Differenzfrequenzen der Originalfrequenzen auftreten und genauso unerwünscht sind. Ich will jetzt nicht ausholen, warum diese u.U. für das Klangbild "schädlicher" sein können, ab wann sie hörbar werden und wie sie sich auf das Hörempfinden auswirken - das ist eine ganz eigene Sache.

Ich bin bei einem neuen Messgerät darauf gestossen, dass es offenbar in der Welt der Audio-Messgerätehersteller nicht klar zu sein scheint, wie man das in den Normen festgeschriebene Mass für diese Intermodulationsverzerrungen, hier spezifisch den sog. Intermodulationsfaktor, ermittelt, wenn man dafür die digitale Messung mit einem Spektrum-Analysator (FFT = Fourier-Frequenzanalyse) verwendet.

Es geht hier um Intermodulation bei Verstärkerschaltungen, nicht um Kreuzmodulation und andere Arten der Intermodulation.

Bei der ursprünglich ausschliesslich verwandten analogen Messmethode wurde in einer Zweiton-Messung mit Hochpassfilter, Bandpassfilter und Demodulation sowie letztlich Effektivwertmessung der Spannung die Gesamteffektivspannung mit einer "True-RMS" Effektivwertmessung der Störprodukte ermittelt und diese zur Effektivspannung der höherfrequenten Tonfrequenzkomponente ins Verhältnis gesetzt. Das ergab den Modulationsfaktor.

Dazu liest man z.B. dieses (aus einem Skript einer FH):
Der Intermodulationsfaktor m_i wird als Mass der Verzerrungen mit zwei Frequenzen f₁ und f₂ gemessen. Nach DIN 45503 geht man zu seiner Bestimmung von der oberen Frequenz f₂ aus, die als mit der niederen Frequenz f₁ moduliert betrachtet wird. Es entstehen als Intermodulationsprodukte:

f2 +/- f1 (2. Ordnung)
f2 +/- 2f1 (3. Ordnung)
f2 +/- 3f1 (4. Ordnung)
...
usw. (i-te Ordnung)

Der Intermodulationsfaktor ist dann das Verhältnis der Effektivspannung für die Summe der betrachteten Intermodulationsprodukte bis zur vordefinierten Ordnung, die man einbeziehen will, zur Effektivspannung des Tons mit der Frequenz f₂ :




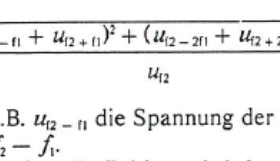
Die gleiche Formel ist z.B. auch in der Grundig Publikation "Messungen an HiFi-Verstärkern nach DIN 45500, D.Elsaesser, Grundig Technische Informationen 1/1970" genannt (dort Intermodulationsfaktor in % angegeben):




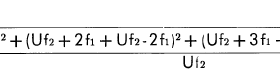
oder ebenso auch auf den Webseiten des Elektroniktutors.de: elektroniktutor.de/elektrophysik/verzerrt.html




Das ist alles dieselbe Formel (es sind nur leicht verschiedene Symbole für die Größen verwendet). Ihr ist gemein, dass zunächst die Einzelspannungen für jeweils die beiden Signale bei den symmetrisch um f2 in den beiden Seitenbändern auftauchenden Intermodulationsprodukten gleicher Ordnung linear addiert werden. Aus den so gewonnenen Spannungen für jede Ordnung wird anschliessend die Summenspannung durch geometrische Addition gebildet.
Im englischen Sprachraum wird geometrische Addition auch rms-Addition genannt (rms=root mean square). Die beinhaltet, dass die zu addierenden Grössen zunächst quadriert werden, dann die Summe aller dieser Quadrate gebildet wird und schliesslich aus dieser Summe der Quadratwerte die Quadratwurzel gezogen wird.
"Geometrische Addition", weil sie der Ermittlung der Hypothenusenlänge aus Ankatheten- und Gegenkatheten-Länge bei einem rechtwinkligen Dreieck entspricht (Satz des Pythagoras).

Während die lineare Addition zweier gleichgroßer Werte in der Summe eine Verdopplung in der Summengröße ergibt (also Faktor 2x oder im Dezibel-Mass = +6 dB), ergibt die geometrische Addition dafür als Summe nur den Wert von (Quadratwurzel aus 2) x Einzelwert, also nur das 1,414-fache (im Dezibel-Mass sind das nur +3 dB) statt des Doppelten. DAS ist der Knackpunkt der Sache, um die es hier noch geht.

Warum werden die Intermodulationsprodukte, die zur selben Ordnung gehören (symmetrich in den Seitenbändern von f₂) linear addiert, aber die Summen verschiedener Ordnung geometrisch addiert?
Eine allgemeine Begründung dafür wird i.a. daraus abgeleitet, ob die zu summierenden Signale untereinander in einer festen Phasenbeziehung stehen. In dem Fall sagt man, sie seien korreliert. Oder ob sie keine feste (konstante) Phasenbeziehung zueinander haben, dann sind sie unkorreliert. Sind die Signale korreliert, addieren sich die Werte linear. Sind sie nicht korreliert, addieren sie geometrisch. Zum Beispiel sind f₁ und f₂ i.a. nicht korreliert, die Effektivspannungen von beiden addieren sich geometrisch (haben f₁ und f₂ gleichen Effektivwert, hat das Summensignal aus beiden nur den 1,41-fachen Effektivwert, ist also nur um 3 dB höher, nicht um 6 dB).

Wenn die o.g. Formel für den Intermodulationsfaktor stimmt, müssen demnach die beiden +/- Seitenbandsignale derselben Ordnung (z.B. f₂ + f₁ und f₂ - f₁) in einer festen/konstanten Phasenbeziehung zueinander und zu f₂ stehen, aber Seitenbandsignale verschiedener Ordnung nicht.

Ich habe dazu nicht viel mehr gefunden. Wer kennt dafür die Herleitung?

Es gibt lediglich in der TGL 17175-04 (dem DIN-Equivalent in der ehemaligen DDR) zur Messung des Intermodulationsfaktors bei Verstärkern eine Anmerkung, dass die IM-Produkte derselben Ordnung als Herkunft den (= den selben?) Amplituden-Modulationsmechanismus haben, der deren lineare Addition (statt sonst erforderlicher geometrischer Addition) begründen soll:



...Immerhin etwas.
Nur selbst das ist etwas dünn.
Hat jemand vom Forum eine ausführlichere Begründung dazu?


Diese Begründung scheint aber - besonders im angelsächsischen Raum - nicht Allgemeingut zu sein. Jedenfalls finde ich dort mehrfach eine andere Formel für den Intermodulationsfaktor, nämlich die, nach der ALLE Intermodulationsprodukte geometrisch aufaddiert werden, unabhängig davon, ob sie zur gleichen Ordnung oder zu verschiedenen Ordnungen gehören, z.B. bei Virtins Technology (Multi-Instrument):




Wenn die in der TGL genannte Begründung zutrifft, kann diese zuletzt gezeigte Summierung ja nur falsch sein. Sie liefert einen um 3 dB zu kleinen (zu guten) Intermodulationsfaktor. Immerhin bin ich doch erstaunt, dass die Fachwelt (?) sich nicht einig zu sein scheint.

Ich bin darauf gestoßen, weil mein neues Messgerät (QuantAsylum QA 403) eben genau um 3 dB besseren Intermodulationsfaktor über dessen eigene Software (v. 1.197) ausgibt als die Messoftware ARTA mit einer Soundkarte als Messgerät, obwohl die zugrundeliegenden FFTs, also die Messung selbst, in beiden Fällen praktisch genau gleich sind. Der 3 dB Unterschied ist also ausschliesslich das Ergebnis der bei Quant Asylum (bislang) verwendeten rein geometrischen Summierung, während ARTA die schon zu Anfang genannte gemischte linear/geometrische Summierung verwendet, die z.B. auch von Grundig genannt und verwendet wurde:



Möglicherweise finden sich in den Standards/Normen auch ausserhalb der genannten TGL erhellende Hinweise. Dies sind z.B.

DIN EN IEC 60268-3:2019-02
oder
SMPTE RP 120 (2005)

Leider habe ich keinen Zugang dazu. Der enorme Preis, der für die Bestellung dieser Dokumente aufgerufen wird, verhindert, dass ich dort nachsehen könnte.
Hat jemand Erkenntnisse dazu, ob in diesen Dokumenten die entsprechende Berechnungs-Formel und deren Begründung enthalten ist?

Hier noch ein praktisches Mess-Beispiel:

Messung gemäss SMPTE, 60 Hz : 7 kHz, Amplitudenverhältnis 4:1 (die Amplitude des 7 kHz Tons ist um 12 dB tiefer als die des 60 Hz Tons). Der 60 Hz Ton hat eine Effektivspannung von 1,0 Veff.
Es handelt sich um Intermodulation, die im Messgerät selbst bei einer Loop-back-Messung stattfindet.
Bei 7 kHz ist das f₂ Signal mit -12 dBV
Bei 7060 Hz und bei 6940 Hz sind die beiden Intermodulationsprodukte (2. Ordnung) mit jeweils -124,5 dBV, also -112,5 dBV unter dem f₂-Pegel.
Es sind auch noch höhere IM-Produkte erkennbar, mit kleinerer Amplitude, die ich hier für die Rechnung in diesem Beispiel der Vereinfachung wegen nicht mitnehme. D.h. ich rechne und messe nur für die Intermodulation 2. Ordnung.

Sieht so aus:




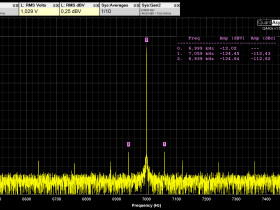
Die Software QA 403 (v. 1.197) errechnet daraus IMD2 (2. Ordnung): IMD2 = -109,5 dB




Wende ich allerdings die Formel nach DIN (Grundig, ARTA) an:

...dann addieren sich beide Werte bei 6940 Hz und 7060 Hz von je -112,5 dB relativ zum 7 kHz Signal linear (da beide 2. Ordnung) zur um 6 dB grösseren Summe auf -106,5 dB. Das QA 403 Ergebnis hätte, um kompatibel zu sein, deshalb -106,5 dB sein sollen, statt -109,5 dB.

Die Differenz zur Messung nach DIN, ARTA, Grundig,... ist demnach 3 dB. Eben weil die QA403-Software die Summierung vollständig geometrisch durchführt, statt zunächst innerhalb der selben Ordnung paarweise linear zu summieren. Nun, wenn man das weiss, kann man ja noch nachträglich immer 3 dB korrigieren.

Dennoch, ich bin und bleibe irritiert.

Wer weiß mehr zu dieser störenden Uneinheitlichkeit?


Besten Gruß
Reinhard

Hallo Andreas,

ich habe bei der Literatursuche gesehen, dass Intermodulation im Sender/Empfängerbereich und auch bei Lautsprechern und Mikrofonen ein wichtiges Thema ist. Aber dort liegt der Schwerpunkt der Fragestellung anders und die Messmethoden weichen auch ab. Zu Empfängern hatte ich ja angemerkt...keine Kreuzmodulation, sowas meine ich in diesem Fall nicht. Die Sender-Leute interessiert z.B. Intercept point usw., andere Baustelle.

Mir geht es wirklich eng um NF-Audio Intermodulation nach der SMPTE 2-Ton-Messung in Verstärkern. Und dabei eigentlich auch nur um die genaue Definition der Berechnungsformel bei Messung mit dem Spektrum-Analysator. Die allgemeine Ausdrucksweise, wie "die Summe der Effektivspannungen der Intermodulationsprodukte wird zu der Effektivspannung des höherfrequenten Tonsignals ins Verhältnis gesetzt" führt nicht weiter. Die Frage dazu ist nämlich genau WIE und WARUM.

Dass man bei der Addition der Effektivspannung zweier Sinustöne bei korrelierten Signalen 6 dB Zuwachs bekommt, aber bei nicht-korrelierten Signalen nur 3 dB, ist ja schon selbst nicht von vornherein ganz trivial. Und hier geht es noch darum, warum das bei Intermodulationsverzerrungen ganz anders als bei harmonischen Verzerrungen ist und warum.

Ich weiß nicht, ob sowas Standard-Lehrstoff im Elektrotechnik-Studium ist (unter "Nicht-lineare Systeme"). Vielleicht nicht. Ist sonst schwer verständlich, dass Firmen, die auf Entwicklung von Hardware und Software für Audio-Analyzer spezialisiert sind, Schwierigkeiten damit haben.

Beispiel dafür:
Formel zur Berechnung der SMPTE Intermodulationsverzerrungen im Benutzer-Handbuch der Fa. Virtins Technology für deren Mess-Software "Multi-Instrument (Autor: Chefentwickler Wang Hongwei, PhD)"

A) im Jahr 2020:



B) im Jahr 2024 (an der gleichen Stelle im gleichen Handbuch, lediglich neue Auflage/Versionsnumme):



Was für ein "Sinneswandel" dieses Autors in den letzten 4 Jahren! In keinem der beiden Fälle wird eine Erklärung gegeben. Für den Sinneswandel auch nicht.
An einer Änderung der Norm oder des Prüfstandards kann es nicht liegen. Die Messmethode besteht schon so seit Ende der 60iger Jahre, war schon Bestandteil der alten DIN 45500 HiFi-Norm. Der darauf bezogene Grundig Artikel mit der letzten Formel datiert z.B. vom Quartal 1 / 1970.

Im Skript der Fachhochschule, die ich im www gesehen habe, wird nur die Formel (B) angegeben, ohne Erläuterung, wie man zu der kommt und warum es nicht Formel A) sein kann/darf. Nach der Devise: Stur auswendig lernen! Mehr müsst Ihr nicht wissen.

Firmen wie Rohde & Schwarz und Audio Precision drücken sich "kryptisch" aus, so dass ich jedenfalls nicht erkennen kann, wie sie es denn ganz genau praktizieren. Diesen beiden würde ich allerdings blindlings zutrauen, dass sie es richtig machen (Formel B). Aber sich davon überzeugen, heisst, man muss deren Gerät benutzen und messen und nachrechnen. Die Handbücher sind nicht präzise genug um daraus abzuleiten, ob denn die Formel A) oder die Formel B) benutzt wird. Messung nach SMPTE Standard schreiben alle. Das sagt auch nicht genug aus.


Gruß
Reinhard

Keiner kann dazu mehr sagen?

Ich habe weiter gesucht.
Über diese Aussagen, bzw. Folgerungen von mir, bin ich aber in den mir zugänglichen Quellen nicht hinausgekommen:

1. Spannungen von nicht-korrelierten Quellen ("nicht-korrelierte Signale") addieren sich geometrisch. D.h. Bei Addition von zwei gleichgroßen Spannungen steigt die Summenspannung auf das 1,4-fache (Wurzel aus 2 = +3 dB). Es wird (geometrische, orthogonale) rms-Addition angewendet.
   
2. Beispiel (nicht-korreliert): Ein Sinus-Ton aus einem ersten Signalgenerator mit der Frequenz f1 und ein Sinus-Ton aus einem zweiten Signalgenerator mit der Frequenz f2 sind i.a. nicht korreliert, sie sind i.a. unabhängig voneinander, z.B. variiert die Phasenlage beider statistisch zueinander. Das Rauschen von verschiedenen Rauschquellen (z.B. von verschiedenen Schaltungsteilen oder Bauteilen) ist unkorreliert (statistisch unabhängig).
   
3. Korreliert sind zwei Quellen ("Signale"), wenn sie nicht unabhängig voneinaner variieren können. Eine Änderung z.B. der Amplitude des Signals einer Quelle ist dann immer auch mit einer Änderung der Amplitude des Signals der anderen Quelle verbunden (gegenseitige Abhängigkeit). Es wird lineare Addition angewendet (Summe von zwei Quellen mit gleichem Pegel verdoppelt sich = + 6 dB)
   
4. Beispiel (korreliert): Die von zwei nebeneinander stehenden gleichen Lautsprechern abgestrahlten Tonsignale, wenn sie von derselben Quelle (Verstärker) stammen, sind korreliert, ihre Amplituden addieren sich in der Weise, dass die Summe um +6 dB grösser ist.
   
5. Intermodulationsverzerrungen von zwei (und mehr) Tönen (Frequenzen, Sinus) entstehen nach dem Mechanismus der Amplitudenmodulation. Dabei sind in der aus der Amplitudenmodulation resultierenden Spektralfunktion (Fourier-Transformierte) die beiden Ausgangsfrequenzen und (wenigstens, 2. Ordnung) zwei neue Frequenzen, nämlich f2+f1 und f2-f1 (=Intermodulationsverzerrung) enthalten. Diese beiden neuen Signale sind nicht voneinander unabhängig. Sie haben denselben Ursprung, gleiche Amplitude und eine feste (keine statistisch variierende) Phasenlage zueinander (die mathematische Herleitung der Funktion der bei Amplitudenmodulation entstehenden Intermodulationsprodukte ergibt den gleichen Amplitudenfaktor für die neuen Signale derselben Ordnung in den beiden Seitenbändern).
   
6. Aufgrund von 5. sind die Intermodulationsprodukte gleicher Ordnung in beiden Seitenbändern miteinander korreliert. Sie können sich nicht unabhängig voneinander ändern.
   

Die Punkte 5. und 6. bedingen Formel B) im letzten Beitrag für die Regel zur Aufsummierung für die Ermittlung des Intermodulationsfaktors mit einem Spektrum-Analysator.
saba-forum.dl2jas.com/index.ph…chment/9803-Formel-6-png/

Bitte gerne Einwände und Ergänzungen !


Weder gängige Lehrbücher ( z.B. der "Tietze-Schenk") noch Informationsschriften der meisten Hersteller (z.B. white papers von Rohde & Schwarz) verweisen explizit auf Formel B. Während sie bei harmonischen Verzerrungen die für Klirrfaktor, bzw. THD die dafür zutreffende Formel (dort gemäss Formel A) noch angeben, schweigen sie leider zu der expliziten Formel für 2-Ton-Intermodulationsverzerrungen. Auch im angelsächsischen Raum scheint diese "Lücke" zu bestehen; und so kommt es dann zu der beschriebenen Verwirrung, dass selbst nagelneue Mess-Software diesbezüglich fehlerhaft sein kann.

Nicht nur ARTA (artalabs.hr/) macht es richtig (Formel B), sondern auch REW (v. 5.30.9) (Room EQ Wizard, roomeqwizard.com/). Bei beiden für Soundkarten geeigneten Programmen habe ich es nachgeprüft. Im ARTA Handbuch ist die korrekte Formel (Formel B) ausdrücklich angegeben. Im REW Help-Menü ist keine Formel angegeben, aber die erhaltenen IMD-Messwerte sind mit REW exakt identisch zu denen mit ARTA.

Das Programm Multi-Instrument (virtins.com/multi-instrument.shtml) sollte jetzt in der neuesten Version V. 3.9.9 auch korrekt arbeiten, wenn man der neuen Help/Handbuch-Publikation für dieses Programm von 2/2024 glaubt. (virtins.com/doc/Measurements-o…sing-Multi-Instrument.pdf)
Die Überprüfung war von mir nicht möglich, da dies Programm meine Soundkarte und den ASIO Treiber meiner Soundkarte nicht erkennen wollte. Dadurch war die Konfiguration der Ein-Und Ausgänge verhindert. Die Bedienung fand ich zudem (im Vergleich mit ARTA und REW) sehr unübersichtlich.

Die Software für Quant Asylum QA403 (QA 40x) hat in der Version 1.197 noch die falsche Formel (Formel A) implementiert, zeigt also deshalb - trotz korrektem FFT (Spektralanalyse) - den Intermodulations-(Verzerrungs) Abstand (gegenüber dem Referenzträger f2) gemäss SMPTE-IMD um 3 dB zu groß (zu gut) an, wie im Startbeitrag gezeigt. Vielleicht wird das in einer späteren Version ja noch berichtigt.

Gruß
Reinhard

RightMark Audio Analyzer (RMAA)


audio.rightmark.org/index_new.shtml

diese Soundkarten - Mess-Software russischen Ursprungs scheidet die Geister. Sie kann nur wenige Eigenschaften messen, ist dafür aber äusserst einfach im Anschluß und in der Bedienung. Es ist lediglich der Pegel am Soundkarten-Master-Volume in einem Vortest 1 dB unterhalb der Klippinggrenzeeinzustellen. Diese wird in einer grün/rot Ampelanzeige signalisiert. Bei mir habe ich die Klipping-Grenze von RMAA bei genau 1 Veff festgestellt. Hat man das richtig gemacht, sind danach die Pegel in dBV definiert (0 dBV = 1 V eff).

Kritiker bemängeln, RMAA würde nicht reproduzierbare Werte liefern oder Werte, die von Messungen mit professionellen Audio-Messgeräten stark abweichen und einges mehr. Nicht alle Kritik ist fair. Generell ist die richtige Anbindung und Kalibrierung von Soundkarten in der verwendeten Mess-Software sorgfältig zu machen. Danach darf der Hardware-Master-Pegel an der Soundkarte (wenn es einen gibt) nicht mehr verstellt werden. Es muss mit Messung verifiziert werden, dass 0 dBV in der Software-Anzeige an den Ein-und Ausgängen auch tatsächlich 1,0 Veff entsprechen und dass keine Equalizer oder andere Mixer des PC-Betriebssystem zwischengeschaltet sind, die das Ergebnis verfälschen können. Macht man dabei Fehler, kommt Murks raus. Das gilt aber grundsätzlich für alle Soundkarten-Messungen. Geht man sorgfältig vor, liefert die Soundkartenmessung die gleichen Werte wie im 5-stelligen Preisbereich liegenden professionellen Messgeräte, kommt mit der Meßgrenze nur nicht ganz so weit herunter. Wie weit, liegt am Ende nicht an der Software sondern an der Qualität der Soundkarte. Für die besten Soundkarten (z.B. von RME) kommt man aber auch auf vierstellige Beträge, die dafür aufgerufen werden.

Der Vergleich der Soundkarten-eigenen Intermodulationsverzerrung von -78 dB im Beispiel des Audio Interface Steinberg UR242 (unten) und des QuantAsylum QA403 Analyzers (Beispiel im ersten Beitrag) mit seiner IMD von -106,5 dB zeigt die weite Spanne in der Qualität, die sich auch im Preis spiegelt.

Im direkten Vergleich mit Soundkarten Mess-Software der Königsklasse, wie ARTA oder REW, liefert RMAA bei Frequenzgang und Klirrfaktor jedenfalls ähnliche, aber nicht ganz exakte Werte. Mit etwas Erfahrung vermeidet man Übersteuerung des Testgerätes, bzw. erkennt solche an den Ergebnissen. Während der Messung selbst sieht man ausser einem Fortschrittsbalken bei RMAA ja nichts, also erkennt man Störungen oder Übersteuerung erst hinterher.

Nun ist hier ja Intermodulation (60 Hz : 7 kHz, 4:1) das Thema. Gilt auch für andere Frequenz- und Amplitudenverhältnisse.
Der Gesamtpegelwert kann bei RMAA nicht eingestellt werden. Bei dieser Messung ist er so vorgegeben, dass das 60 Hz Signal -5 dBV hat (oder haben soll) und das 7 kHz-Signal -17 dBV. Womöglich bezieht sich das aber auf den vorher schon um 1 dB verminderten Startpegel, so dass tatsächlich mit -6 dBV bei 60 Hz und -18 dB bei 7 kHz gemessen wird. So sieht es jedenfalls im Frequenzspektrum aus (FFT). An der Stelle besteht zumindest schon mal eine Ungewißheit.

Im Loop-Back Test an meinem Audio-Interface Steinberg UR 242, gibt es für den 60 Hz / 7 kHz 4:1 SMPTE Intermodulationstest mit RMAA in der Ergebnisausgabe unter "IMD + noise" eine nicht gängige Bewertung. Demnach soll die Summe aus Rauschspannung und IMD-Verzerrungen unglaublich geringe 0,0042 % betragen, das wären -87 dB.

RMAA IMD Werte.png

Einerseits macht die Zusammenführung von Rauschen mit Intermodulation wenig Sinn, wenn man nur an den IM-Verzerrungen interessiert ist, andererseits kann man auch sofort in der Spektraldarstellung sehen, dass die Intermodulationsverzerrungen sehr viel grösser sind als von RMMA in der Ergebnistabelle gelistet. Die Spektraldaten der Fourieranalyse offenbaren die wahren, viel stärkeren IMD-Verzerrungen:

RMAA: IMD3 = -78 dB, 0,012 %




Es dominieren die beiden symmetrischen Intermodulationsprodukte 3. Ordnung in den beiden Seitenbändern, die beide bei -102 dBV liegen. Deren Summe (Verdopplung) ergibt -102 dB + 6 dB = -96 dB.
Der Abstand der Summe zum 7 kHz Träger (-18 dBV) beträgt 18 dB - 96 dB = -78 dB. Die dominierenden Intermodulationsverzerrungen 3. Ordnung (ohne Rauschen) liegen demnach bei IMD3= -78 dB, das sind ca. 0,012 %.

Der Ergebniswert, der von RMAA in der Zusammenfassung als 0,0042 % für IMD + noise angegeben wird, ist anhand des von RMAA gemessenen FFT in der Spektralanalyse absolut nicht nachvollziehbar, ist Murks.


Die Signalstärken und Frequenzen der Signale imn der Frequenzanalyse von RMAA sind allerdings korrekt. Für den gleichen Pegel (-6 dBv für 60 Hz und -18 dB für 7 kHz) ergeben ARTA und REW identische Frequenzanalyse-Ergebnisse wie RMAA:

ARTA: IMD3 = -78 dB, 0,011 %





REW: IMD3 = -78 dB, -0,0099 %




Die leichte Abweichung mit RMAA (IMD3 = 0,012 %) gegenüber 0,010 % (+/- 0,001%) mit ARTA und REW, ist noch im Rahmen der Genauigkeit, die man erwarten kann.
Nur berichtet RMAA leider nicht diesen korrekten (wahren) Wert sondern eine ganz andere, viel zu kleine unbrauchbare Hausnummer "0,0042 %". Was dieser Wert soll, können wohl nur die Erschaffer von RMAA erklären.


Man muss also bei RMAA aufpassen, wofür man es einsetzt und müsste die damit erhaltenen Werte durch Messung mit einer unabhängigen Software erst mal validieren. Wie, geschrieben, für THD Messung mit RMAA habe ich das gemacht, dort stimmen die Werte innerhalb +/- 0,002 % überein.

Bei den anderen Messwerten sieht es im Vergleich so aus:

Frequenzgangabweichung
20 Hz RMAA = +0,02 dB / ARTA = -0,1 dB
20 kHz RMAA = -0,27 dB / ARTA = -0,28 dB

Noise 48 kHz BW RMAA = -101 dBV / ARTA = -95,0 dBV / REW = -94,9 dBV

Dynamic Range RMAA = 101 dB / ARTA = 90-96 dB SINAD (15-16 bits ENOB) / REW = 90-96 dB SINAD (15-16 bits ENOB)

THD 1 kHz, -3 dB RMAA = 0,0034 % / ARTA = 0,0025 % / REW = 0,0027 %


Auch das Rauschen wird demnach von RMAA deutlich als besser als tatsächlich bewertet. Der mit RMAA ermiitelte Dynamikumfang wird von RMMA leicht besser ermittelt als mit ARTA und REW, dort habe ich aber eine empfindlichere Methode (31-Multiton, 3/Oktave) verwendet, in die Intermodulationsverzerrungen zusätzlich eingehen.

RMAA ist demnach nur beschränkt brauchbar. Es gibt dort für bestimmte Werte, insbesondere bei der Intermodulation, nicht erwartete starke Abweichungen im Auswerte-Rechenteil der Software, was das Ausrechnen/Überprüfen "zu Fuß" aus dem FFT-Spektogramm erfordert.

Hallo Rolf,

schön, dass Du dazu was sagst und auch bestätigst, dass die RMAA IMDs so klein ausfallen.
Ich habe genau gemessen und auch gerechnet. Jetzt konnte ich die Unklarheit auflösen. Es ist so:

1. Der Unterschied zwischen RMAA IMD und der SMPTE (DIN)-Methode beträgt 9 dB ( = Faktor 2,82).

Dazu Beispiel oben die Spektren an denen man das nachprüfen kann und für die ich ja auch die RMAA-Werte gepostet habe:

RMAA: 0,0042 % IMD
SMPTE: 0,010 % (+/- 0,001%) IMD

Check: 2,82 x 0,0042% (RMAA) = 0,012 % (SMPTE)
passt also!


2. Das kommt daher:

RMAA verwendet zwar 60 Hz : 7 kHz im Verhältnis 4:1, genauso wie die SMPTE-Methode. Aber RMAA wertet über das Leistungsverhältnis zur Gesamtleistung als Referenz aus (sog. Power-Methode), während SMPTE (DIN) nach Spannungsverhältnis zur Spannung der höherfrequenten Komponente (nur dieser!) auswertet. Es ist leicht zu zeigen, dass der Unterschied beider Methoden genau die genannten 9 dB ausmacht.

In den nachfolgenden Formeln steht das große I für "Magnitude". Man kann dafür die Effektivspannung Ueff einsetzen, die die betreffende Spektralkomponente jeweils hat.

Power-Methode:


In der Formel der Power Methode kann man in guter Näherung in diesem Fall (4:1 Verhältnis der beiden Mess-Signale) und bei 20 kHz Bandbreite und nicht sehr großer Intermodulation so vereinfachen:




Jetzt vergleichen mit der SMPTE (DIN) Methode:



Dies sind die Unterschiede:

1. Bei der Power Methode werden die Spannungswerte aller IM-Produkte geometrisch aufaddiert (Summe der Quadratwerte und aus der Summe dann die Wurzel) und die resultierende Summe auf die Spannung des 60 Hz Signals bezogen.

2. Bei der SMPTE (DIN) Methode werden die Spannungswerte der IM-Produkte gleicher Ordnung erst linear addiert und danach die so erhaltenen Summen geometrisch addiert. Durch die lineare Summierung der Paare gleicher Ordnung ist die Summe der IM-Verzerrungswerte um 3 dB größer als bei geometrischer Addition aller IM-Produkte (das hatte ich vorher ja schon ausführlich erläutert). Da die Endsumme nur auf den Pegel des 7 kHz Signals bezogen wird und nicht auf den Gesamtpegel, gibt das ein um 12 dB größeres Verhältnis. Insgesamt ergibt sich aus den beiden Effekten eine netto-Bilanz von (+3 dB - 12 dB) = - 9 dB für die IM Verzerrungen nach der Power-Methode gegenüber Berechnung mit der SMPTE/DIN-Methode.

Ich habe das eben nochmal praktisch mit Messungen gem. Power-Methode und SMPTE-Methode nachgeprüft. Auch in den Messungen 9 dB Unterschied.


Wenn Du nur einen Unterschied von 6 dB gefunden hast...kann es daran gelegen haben, dass Du bei Deiner Rechnung wie in der Power-Methode (alle Produkte geometrisch) addiert hast das ergibt eine 3 dB zu kleine Summe) aber richtig auf das 7 kHz Signal bezogen hast. Dann ist der Unterschied zu RMAA nur 6 dB. Du hast dann also in Deiner Rechnung nicht die SMPTE-Formel angewandt sondern diese, allerdings nur auf 7 kHz (f2) bezogene, "Power"-Formel:



Ich glaube. die wurde sogar mal von der IEEE als Alternative vorgeschlagen, hat es aber nach meiner Kenntnis nicht zu einem "Standard" wie SMPTE/DIN geschafft.


Am Ende ist also RMAA so was wie rehabilitiert. Denn RMAA behauptet ja nicht, die IMD-Werte gemäss SMPTE oder DIN anzugeben. Die sagen einfach gar nichts dazu, wie sie rechnen. Und ich hatte wegen der Signale 60 Hz : 7 kHz im Verhältnis 4:1 voreilig angenommen, es würde sich bei der Methode in RMAA deshalb um Messung nach SMPTE handeln. Tatsächlich ist es aber eine Messung nach der Power-Methode. Und dann "stimmen" die ausgewisenen Werte. Nur kann man sie nicht mit IMD-Werten anderer Messungen vergleichen, wenn man die Messmethode und die Berechnungsmethoden im Einzelfall nicht genau kennt und daher nicht umrechnen kann. Die sind aber oft gar nicht angegeben.

Da wegen der unterschiedlichen Auswertungsmethoden (Berechnungsmethoden) für IMD aus den Signalen eines Echtzeitanalysators / Spektrumanalysators, selbst bei ein und demselben (technischen) Messverfahren, die Werte für Mehrtonverzerrungen so oft leider nicht vergleichbar sind, hat das dazu geführt, dass Intermodulationsverzerrungen vielen als "nutzlos" erscheinen und oft auch gar nicht (mehr) gemessen oder angegeben werden. Es wird auch oft gesagt, sie seinen "kompliziert zu messen". Das stimmt aber nicht mehr, heute ist das sehr einfach und kostet auch nichts extra. Ich vermute, dass viele sich auch nicht weiter damit befassen wollen, weil aufgrund der vielen unterschiedlichen Standards die Eindeutigkeit und Übersichtlichkeit gelitten hat.

In einem anderen Forum hiess es: "Intermodulationsverzerrungen? Wozu braucht man das? THD ist doch viel einfacher und sagt bereits alles."

Das teile ich persönlich so nicht. Aber die nicht vergleichbaren Werte haben mich ja auch gestört. Letztlich kann man sich da - so wie hier - näher mit beschäftigen und in das Thema reinfressen. Mir ist jetzt dadurch vieles klarer. Vielen ist das aber schon zu viel Aufwand.

Ich glaube, dass oft einfach ein/das vorhandene Messgerät verwendet wird, ohne dass vom Nutzer wirklich verstanden ist, was er damit eigentlich misst, besonders wenn ganz unterschiedliche Datenauswertungs-Methoden dahinter stehen, die auch noch sehr verschiedene Ergebnisse liefern, wie besonders bei der Messung von Intermodulationsverzerrungen. Und davon sollte man wohl auch Tester bei Zeitschriftenverlagen nicht von vornherein ausnehmen.
Bei RMAA ist die Gefahr besonders groß, weil es so schön einfach verwendbar ist, aber gleichzeitig als black-box ohne Dokumentation und ohne viel Kontrollmöglichkeit daherkommt.

Gruß
Reinhard

Hallo Rolf,

was Du sagst...Tuner...ja die sind eine ganz eigene Kategorie, was NF-Intermodulation betrifft. Was Tuner aus den 1970iger und bis in die 1980iger Jahre angeht, die haben überwiegend schlechte NF-IMD (DIN/SMPTE) von typisch 1% - 2,5 %, selbst wenn der gemessene Klirrfaktor mit <0,2% für Tuner ganz gut ist. Absolute Spitzenklasse (Accuphase...) hier mal ausgenommen. Selten habe ich mal um 0,5% IMD hinbekommen. Ich bin glücklich, wenn ich mit bestmöglichem Abgleich auf < 1% IMD komme, es gibt auch schlechte Fälle, die bei 3-5% liegen. Bessere/neuere Tuner, wie den guten GRUNDIG Fine Arts T 9000 habe ich daraufhin noch nicht geprüft, der sollte eigentlich besser bei den NF-IM-Verzerrungen abschneiden.

Nicht zu verwechseln mit den sog. Pilottonverzerrungen (9 kHz moduliert, "Intermodulation nach IEEE 185-1975, Abschnitt 7.6.3"), die zahlenmässig mit 0,1-0,2% meist gut ausschauen.


Hallo Michael,

bei uns in Europa (wenigstens, SABA, Grundig, usw.) finden wir IMD ab Ende der 60iger Jahre meist angegeben. Ob das in USA auch so war?
Dann kam in den späteren 70iger Jahren Otala mit TIM (DIM), dynamischen Intermodulationsverzerrungen dazu. Gleichzeitig wurden die Schaltungen immer verzerrungsärmer und Klirrfaktor, IMD und DIM sanken bis nahe an die Grenze des Messbaren.

Es hat sich dann herausgestellt, dass es praktisch keine Fälle mit auffällig erhöhtem IMD und DIM gibt, wenn THD, insbesondere oberhalb 10 kHz, bei mittlerer Leistung (ca. 1-10 W) bis Nennleistung sehr niedrig ist (<0,03 %). Daraus ist ja nachvollziehbar, wenn heute nicht mehr so starkes Interesse an IMD und DIM besteht, wie in den 1970iger und 80iger Jahren.

Aber bei unseren Vintage-Schätzen, die das heute Machbare noch nicht ausloten, bin ich auch Deiner Meinung, dass IMD wichtig ist und nicht automatisch niedrig.

IMD erzeugt in einem Multiton-Musikspektrum einen "Teppich" an Intermodulationsprodukten, der sich dem Rauschteppich überlagert und den verfügbaren Dynamikumfang verringert. Heutzutage misst man das ja am allerbesten mit der sog. Multiton-Methode: 31-32 Töne über den Bereich 20 Hz - 20 kHz gleichmässig verteilt gleichzeitig, alle mit gleichem Pegel. Dann schaut man, wie groß der Abstand der Spitzenwerte vom Untergrund noch ist, der von IMD zugemüllt wird. Dieser Abstand (entspricht etwa SINAD über den gesamten Frequenzbereich), geteilt durch 6, gibt den ENOB, den Dynamikumfang in bits.

Typisch für Mittelklasse HiFi-Vollverstärker und Endstufen (überwiegend eigene Messungen):
Mitte 1960iger Jahre: Multiton-Abstand ca. 70-80 dB, ENOB 11-13 bits, THD ca. 0,2-0,5 %, IMD(SMPTE) ca. 0,5-1 %, DIM(100) ca. 0,2-0,5%
Mitte 1970iger Jahre: Multiton ca. 90-100 dB, ENOB 15-17 bits, THD ca. 0,02-0,1 %, IMD(SMPTE) ca. 0,1-0,3 %, DIM(100) ca. 0,04-0,1 %
Mitte 1980iger Jahre: Multiton ca. 95-105 dB, ENOB 16-17 bits, THD ca. 0,002-0,01 %, IMD(SMPTE) ca. 0,01-0,1 %, DIM(100) ca. 0,001-0,1 %
2023 (beste Oberklasse): Multiton ca. 110-120 dB, ENOB 18-20 bits, THD ca. 0,0002-0,001 %, IMD(SMPTE) < 0,001%, DIM(100) < 0,001 %.

Der gemäss Audio Science Review derzeit (März 2024) bzgl. Verzerrungen und Signal-Rauschabstand "beste" Vollverstärker soll der Topping LA90 Discrete (= D Model) sein, aus chinesischer Audio-Schmiede. Leider hat er keine Klangregler.
audiosciencereview.com/forum/i…e-amplifier-review.43756/


Grüße
Reinhard

KOR schrieb:

Bei 8 Ohm sind die Werte deutlich niedriger, selbst bei gleicher Leistung. Es gibt da offensichtlich ein Zusammenhang mit den Strömen, die von der Endstufe geliefert werden müssen.

ENOB bzw. Multiton kannte ich noch nicht, macht aber sehr viel Sinn. Meistens sind es ja mehr als zwei Frequenzsignale, die ein Verstärker verarbeiten muss. Das zeigt aber auch, dass die Technik der 70er schon "digitalfest" war. Die ersten CD-Player hatten oft nur 14 Bit.

An 8 Ohm Last sind die Verzerrungen fast immer deutlich besser als an 4 Ohm, auch bei gleicher Ausgangsleistung - ja das kann ich auch bestätigen. Kleinere Stromstärke gibt bessere Werte. Spannung hat meist den kleineren Einfluß.


Multiton-Test Beispiele

Definition ENOB: de.wikipedia.org/wiki/Effektive_Anzahl_von_Bits
Vereinfacht: SINAD/6

1. Körting Low-Fi Stereo-Verstärker (1969/1970 , aber noch Schaltungs-Technik von 1965/66):
an 4 Ohm Last

70 dB Dynamikbereich = ENOB 11 bits

2. Douk Audio, Nobsound, P1 Röhren-Vorverstärker, KH-Verstärker (low-budget, mit Röhren-Impedanzwandlerstufe, 2022), KH-Ausgang an 30 Ohm Last:

80 dB Dynamikbereich = ENOB 13 bits

3. Topping L30 II qualitativ hochwertiger KH-Verstärker (Spitzenklasse, 2023), KH-Ausgang an 30 Ohm Last:

120 dB Dynamikbereich = ENOB 20 bits
Hier kommt meine Messung an seine eigene Grenze, da mein Analyzer selbst nur bis 125 dB "kann". Kommen dann noch kleine Störungen vom Steckernetzteil drauf - wie hier - wird dadurch der Messwert zusätzlich beschränkt. Messung dieses Verstärkers an einem 50'000 $ teuren Audio Precision APx555 Audio-Analyzer bescheinigen dem Topping L30 II sogar 126 dB = 21 bits ENOB.
audiosciencereview.com/forum/i…view-headphone-amp.36027/


Diese Multitonmessungen sind wirklich auf Anhieb sehr anschaulich, nackte IMD-Werte weniger. Du siehst am Multiton-Screenshot des Frequenzspektrums sofort, was hot oder Schrott ist, um das mal so ganz salopp zu sagen.

Gruß
Reinhard

Quant Asylum hat vor wenigen Tagen in einer neuen Software (v. 1.198) für seinen Audio Analyzer QA40x die Datenverarbeitung für IMD Messungen nach DIN/SMPTE in dem Sinne geändert, wie ich es oben angesprochen hatte.
Damit liefert jetzt auch der Quant Asylum QA40x (derzeit neueste Hardware ist QA403) die gleichen mit DIN / SMPTE kompatiblen Intermodulations-Verzerrungs-Messwerte, wie sie auch mit ARTA und REW erhalten werden und eine Korrektur-Umrechnung ist ab Software v. 1.198 nicht mehr nötig.

RMAA (Right Mark Audio Analyzer) IMD-Messwerte sind und bleiben- wie oben ausgeführt - gegenüber DIN /SMPTE IMD-Werten nach wie vor 9 dB tiefer.

Gruß
Reinhard